نماهای صحیح مثبت

ساده‌ترین نوع توان، با نماهای صحیح مثبت است. نما بیانگر این است که پایه چند بار باید در خود ضرب شود. برای مثال 3⁵ = 3 × 3 × 3 × 3 × 3 = 243. در اینجا 3 پایه و 5 نما است، و 243 باب است با 3 به توان 5. عدد 3، 5 بار در عمل ضرب نشان داده می‌شود چون نما برابر 5 است.

به طور قراردادی، a² = a×a را مربع، a³ = a×a×a را مکعب می‌نامیم. 3² «مربع سه» و 3³ «مکعب سه» خوانده می‌شوند.

اولین توان را می‌توانیم به صورت a⁰ = 1 و سایر توان‌ها را به صورت aⁿ⁺¹ = a·aⁿ بنویسیم.

نماهای صفر و یک

3⁵ را می‌توان به صورت 1 × 3 × 3 × 3 × 3 × 3 هم نوشت، عدد یک را می‌توان چندین بار در عبارت مورد نظر ضرب کرد، زیرا در عمل ضرب عدد یک تفاوتی در جواب ایجاد نمی‌کند و همان جواب گذشته را می‌دهد. با این تعریف، می‌توانیم آن را در توان صفر و یک هم استفاده کنیم:

• هر عدد به توان یک برابر خودش است.

a¹ = a

• هر عدد به توان صفر برابر یک است.

a⁰ = 1

(برخی نویسندگان 0⁰ را تعریف نشده می‌خوانند.) برای مثال: a^{0= a2-2= a2/a2 = 1 (در صورتی که a ≠ 0)}

^{نماهای صحیح منفی}

^{اگر عددی غیرمنفی را به توان -1 برسانیم، حاصل برابر معکوس آن عدد است.}

^{a−1 = 1/a}

در نتیجه:

a⁻ⁿ = (aⁿ)⁻¹ = 1/aⁿ

اگر صفر را به توان عددی منفی برسانیم، حاصل در مخرج صفر دارد و تعریف نشده‌است. توان منفی را می‌توان به صورت تقسیم مکرر پایه هم نشان داد. یعنی 3⁻⁵ = 1 ÷ 3 ÷ 3 ÷ 3 ÷ 3 ÷ 3 = 1/243 = 1/3⁵.

خواص

مهم‌ترین خاصیت توان با نماهای صحیح عبارتست از:

که از آن می‌توان عبارات زیر را نتیجه گرفت:

از آنجایی که جمع و ضرب خاصیت جابجایی دارند (برای مثال 2+3 = 5 = 3+2 و 2×3 = 6 = 3×2) توان دارای خاصیت جابجایی نیست: 2³ = 8 است در حالی که 3² = 9. همچنین جمع و ضرب دارای خاصیت انجمنی هستند (برای مثال (2+3)+4 = 9 = 2+(3+4) و (2×3)×4 = 24 = 2×(3×4)) توان باز هم دارای این خاصیت نیست: 2³ به توان چهار برابر است با 8⁴ یا 4096، در حالی که 2 به توان 3⁴ برابر است با 2⁸¹ یا 2,417,851,639,229,258,349,412,352.

توان‌های ده

در سیستم مبنای ده، محاسبه توان‌های ده بسیار راحت است: برای مثال 10⁶ برابر است با یک میلیون، که با قرار دادن 6 صفر در جلوی یک به دست می‌آید. توان با نمای ده بیشتر در علم فیزیک برای نشان دادن اعداد بسیار بزرگ یا بسیار کوچک به صورت نماد علمی کاربرد دارد؛ برای مثال 299792458 (سرعت نور با یکای مترمکعب بر ثانیه) را می‌توان به صورت 2.99792458 × 10⁸ نوشت و به صورت تخمینی به شکل 2.998 × 10⁸. پیشوندهای سیستم متریک هم برای نشان دادن اعداد بزرگ و کوچک استفاده می‌شوند و اصل این‌ها هم بر توان 10 استوار است. برای مثال پیشوند کیلو یعنی 10³ = 1000، پس یک کیلومتر برابر 1000 متر است.

توان‌های عدد دو

توان‌های عدد دو نقش بسیار مهمی در علم رایانه دارند چون در کامپیوتر مقادیر را می‌توان برای یک متغیر nبیتی درنظر گرفت.

توان‌های منفی دو هم استفاده می‌شوند، و به دو توان اول نصف و ربع می‌گویند.

توان‌های عدد صفر (0)

اگر توان صفر مثبت باشد، حاصل عبارت برابر خود صفر است:.

اگر توان صفر منفی باشد، حاصل عبارت 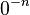تعریف نشده‌است، زیرا تقسیم بر صفر وجود ندارد.

اگر توان صفر عدد یک باشد، حاصل عبارت برابر یک است:.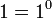

(بعضی از نویسندگان می‌گویند که تعریف نشده‌است.)

توان‌های منفی یک

توان‌های منفیِ یک بیشتر در دنباله‌های تناوبی کاربرد دارد.

اگر نمای عددِ منفیِ یک، فرد باشد، حاصل آن برابر خودش است:

اگر نمای عددِ منفیِ یک، زوج باشد، حاصل آن برابر یک است: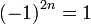

توان‌های اعداد حقیقی مثبت

به توان رساندن عددی حقیقی مثبت به توان یک عدد غیرصحیح را می‌توان به چند صورت به دست آورد:

• عددی کسری تعریف کنیم و ریشه nام را به دست بیاوریم. این روشی است که در مدرسه‌ها از آن استفاده می‌کنند.
• لگاریتم طبیعی تعریف کنیم و سطح زیر نمودار 1/x را به دست بیاوریم.

توان‌های کسری

از بالا به پائین: x^1/8, x^1/4, x^1/2, x¹, x², x⁴, x⁸.

در یک توان، با معکوس کردن نما ریشه آن بدست می‌آید. اگر عدد حقیقی مثبت و n عددی صحیح مثبتی باشد، داریم:

و ریشه nام نامیده می‌شود:

برای مثال: 8^1/3 = 2. حالا می‌توانیم توان 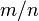را به صورت زیر تعریف کنیم: