سلام اقای فرشباف عقب ماندگی 2هفته ام را با این هفته را به علت نقص کامپیوتر جبران کردم.

hadi جمعه 13 دی 1392 ساعت 19:38

0 نظر

ضرب چندجمله ای ها

توضیح اولیه

فرض کنید میخواهید بدانید حاصل ضرب x در (y+2) چیست؟ قطعه x را در حاشیه عمودی کنار فضای کار و قطعه y و دو مربع سبز را در حاشیه افقی کنار فضای کار قرار دهید. مستطیلی که با خطوط قرمز نشان داده شده را با قطعه های xy و 2x پر کنید. جواب خود را یافتید؟

مقادیر x یا y را با کلیک بر روی اشکال و کشیدن آنها تغییر دهید. می بینید که جواب تغییری نمی کند. یعنی به جای x و y می توان هر عددی قرار داد.

ضرب دو جمله ای ها

با استفاده از اشکال موجود، حاصل ضرب عبارت های زیر را پیدا کنید.

(x+1)(x+2)

(x+1)(y+5)

(x+y)(2x+3y)

قانون توزیع پذیری ( پخشی )

مستطیل را با پاسخ ضرب زیر پر کنید:

x(2y+5)

شکل حاصل، نمایش تصویری قانون توزیع پذیری ( پخشی ) است. یعنی:

x(2y+5)=2xy+5x

مقادیر x یا y را با کلیک بر روی اشکال و کشیدن آنها تغییر دهید.

محورهای افقی و عمودی را پر کنید تا معادله 4x+2y=2(2x+y) را نشان بدهید.

مقادیر x یا y را با کلیک بر روی اشکال و کشیدن آنها تغییر دهید.

hadi جمعه 13 دی 1392 ساعت 19:31

0 نظر

تجزیه عبارات جبری درجه دوم هم آسان شد!

بدون تردید تجزیه عبارات جبری درجه دوم که عموما"به شکل ax²+bx+c نوشته میشوند یکی از مهمترین مهارتهایی است که دانش آموزان دبیرستانی در مقدمات جبر می آموزند و این مهارت کاربرد بسیار وسیعی در قسمتهای مختلف دروس ریاضی دارد.

هر کس به دانش آموزان مقطع پایین دبیرستان تجزیه ی عبارات فوق را درس داده باشد بخوبی میداند که یک دانش آموز در کجای این درس مشکل دارد. مشکل دقیقا" در آنجاست که دانش آموز باید در ذهن خود دو عدد پیدا کند که مجموع و حاصلضرب آنها داده شده است. مثلا" دانش آموز باید دو عدد پیدا کند که مجموع آنها S=7 و حاصلضرب آنها P=12 باشد.(حرف S مخفف Sum و حرف P مخفف Product است)

بدیهی است در اینجا اعداد مورد نظر 3 و 4 هستند. ولی اگر S و P کمی بزرگ باشند، مثلا" دو رقمی و یا حتا سه رقمی و بیشتر باشند، مضافا" آنکه یکی از آنها یا هر دو منفی نیز باشند آنگاه مسئله برای دانش آموز سخت تر میشود و زمان زیادتری لازم است تا او بتواند اعداد مورد نظر را پیدا کند. مثلا" من دانش آموزان زیادی را دیده ام که برای پیدا کردن دو عدد که مجموع آنهـــا S=10 و حاصلضربشان P=-11 باشــــد مدتی بیش از یکدقیقه وقت خواسته اند و در موارد مشکل تر مثل اینکه دو عدد پیدا کنید که مجموع شان S=2 و حاصلضرب شان P=-192 باشد، حتا در زمانی بیش از آن نیز نتوانسته اند جواب را پیدا کنند. در اینگونه موارد دانش آموز ممکن است امیدش را از دست بدهد و مایوس شود. در اینصورت دیگر نمیتوان از او انتظار داشت که به کوشش ادامه دهد. یک آموزگار خوب باید مواظب دانش آموزانش باشد و مطلقا" نگذارد که چنین وضعی برای آنها پیش آید.

اجازه دهید مطلب را با یک مثال ساده دنبال کنم:

مثال یک. عبارت 3x²+7x+4 را تجزیه کنید.

حل. روش کلاسیک حل این مسئله این است که ابتدا دو عدد پیدا کنیم که مجموع شان 7 و حاصلضرب شان 12 باشد. این دو عدد 3 و 4 هستند. مرحله بعد این است که ترم خطی عبارت را بشکنیم بطوریکه عبارت دارای چهار ترم شود و بالاخره با استفاده از روش دسته بندی یا"فاکتور گیری گروهی" عبارت را تجزیه کنیم.

یک روش دیگری هم در اینجا معمول است (که نمیدانم آیا در ایران آنرا تدریس میکنند یا نه) و روش ساده و مناسبی است. در حقیقت باید بگویم که گروه زیادی از دانش آموزانی که از توانایی کمتری در ریاضیات برخوردار هستند، بیشتر تمایل به یاد گرفتن این روش نشان میدهند زیرا یک مرحله کوتاه تر از روش فوق است و در آن نیازی به دسته بندی کردن ترم ها نیست. در این روش عبارت ax²+bx+c را نخست به صورت یک کسر مینویسیم. مخرج کسر a است و صورت کسر مرکب از یک جفت پرانتز است که ترمهای اول آنها ax است. به این شکل:

اینک باید دو عدد پیدا کنیم که مجموع آنها b و حاصلضرب شان ac باشد. وقتیکه این دو عدد را پیدا کردیم( فرض کنیم باشند m و n ) آنها را در داخل پرانتزها و بعد از ax ها میگذاریم، به این شکل:

و در پایان، مخرج کسر را با ضرایب موجود در یک پرانتز(یا اگر لازم باشد با ضرایب موجود در هر دو پرانتز) ساده میکنیم تا مخرج کسر کاملا" ناپدید شود. مخرج کسر همواره ناپدید میشود.

hadi جمعه 13 دی 1392 ساعت 19:08

0 نظر

نماهای صحیح مثبت

ساده‌ترین نوع توان، با نماهای صحیح مثبت است. نما بیانگر این است که پایه چند بار باید در خود ضرب شود. برای مثال 3⁵ = 3 × 3 × 3 × 3 × 3 = 243. در اینجا 3 پایه و 5 نما است، و 243 باب است با 3 به توان 5. عدد 3، 5 بار در عمل ضرب نشان داده می‌شود چون نما برابر 5 است.

به طور قراردادی، a² = a×a را مربع، a³ = a×a×a را مکعب می‌نامیم. 3² «مربع سه» و 3³ «مکعب سه» خوانده می‌شوند.

اولین توان را می‌توانیم به صورت a⁰ = 1 و سایر توان‌ها را به صورت aⁿ⁺¹ = a·aⁿ بنویسیم.

نماهای صفر و یک

3⁵ را می‌توان به صورت 1 × 3 × 3 × 3 × 3 × 3 هم نوشت، عدد یک را می‌توان چندین بار در عبارت مورد نظر ضرب کرد، زیرا در عمل ضرب عدد یک تفاوتی در جواب ایجاد نمی‌کند و همان جواب گذشته را می‌دهد. با این تعریف، می‌توانیم آن را در توان صفر و یک هم استفاده کنیم:

هر عدد به توان یک برابر خودش است.

a¹ = a

هر عدد به توان صفر برابر یک است.

a⁰ = 1

(برخی نویسندگان 0⁰ را تعریف نشده می‌خوانند.) برای مثال: a^{0^{= a^{2-2^{= a^{2^{/a^{2 ^{= 1 (در صورتی که a ≠ 0)}}}}}}}}

^{نماهای صحیح منفی}

^{اگر عددی غیرمنفی را به توان -1 برسانیم، حاصل برابر معکوس آن عدد است.}

^{a⁻¹ = 1/a}

در نتیجه:

a⁻ⁿ = (aⁿ)⁻¹ = 1/aⁿ

اگر صفر را به توان عددی منفی برسانیم، حاصل در مخرج صفر دارد و تعریف نشده‌است. توان منفی را می‌توان به صورت تقسیم مکرر پایه هم نشان داد. یعنی 3⁻⁵ = 1 ÷ 3 ÷ 3 ÷ 3 ÷ 3 ÷ 3 = 1/243 = 1/3⁵.

خواص

مهم‌ترین خاصیت توان با نماهای صحیح عبارتست از:

$a^{m + n} = a^m \cdot a^n$

که از آن می‌توان عبارات زیر را نتیجه گرفت:

$a^{m - n} = \begin{matrix}\frac{a^m}{a^n}\end{matrix}$

$(a^m)^n = a^{mn} \!\,$

از آنجایی که جمع و ضرب خاصیت جابجایی دارند (برای مثال 2+3 = 5 = 3+2 و 2×3 = 6 = 3×2) توان دارای خاصیت جابجایی نیست: 2³ = 8 است در حالی که 3² = 9. همچنین جمع و ضرب دارای خاصیت انجمنی هستند (برای مثال (2+3)+4 = 9 = 2+(3+4) و (2×3)×4 = 24 = 2×(3×4)) توان باز هم دارای این خاصیت نیست: 2³ به توان چهار برابر است با 8⁴ یا 4096، در حالی که 2 به توان 3⁴ برابر است با 2⁸¹ یا 2,417,851,639,229,258,349,412,352.

توان‌های ده

در سیستم مبنای ده، محاسبه توان‌های ده بسیار راحت است: برای مثال 10⁶ برابر است با یک میلیون، که با قرار دادن 6 صفر در جلوی یک به دست می‌آید. توان با نمای ده بیشتر در علم فیزیک برای نشان دادن اعداد بسیار بزرگ یا بسیار کوچک به صورت نماد علمی کاربرد دارد؛ برای مثال 299792458 (سرعت نور با یکای مترمکعب بر ثانیه) را می‌توان به صورت 2.99792458 × 10⁸ نوشت و به صورت تخمینی به شکل 2.998 × 10⁸. پیشوندهای سیستم متریک هم برای نشان دادن اعداد بزرگ و کوچک استفاده می‌شوند و اصل این‌ها هم بر توان 10 استوار است. برای مثال پیشوند کیلو یعنی 10³ = 1000، پس یک کیلومتر برابر 1000 متر است.

توان‌های عدد دو

توان‌های عدد دو نقش بسیار مهمی در علم رایانه دارند چون در کامپیوتر مقادیر $2^n$ را می‌توان برای یک متغیر nبیتی درنظر گرفت.

توان‌های منفی دو هم استفاده می‌شوند، و به دو توان اول نصف و ربع می‌گویند.

توان‌های عدد صفر (0)

اگر توان صفر مثبت باشد، حاصل عبارت برابر خود صفر است: $0=0^2$ .

اگر توان صفر منفی باشد، حاصل عبارت 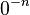$0^{-n}$ تعریف نشده‌است، زیرا تقسیم بر صفر وجود ندارد.

اگر توان صفر عدد یک باشد، حاصل عبارت برابر یک است: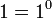 $1=1^0$ .

(بعضی از نویسندگان می‌گویند که $0^0$ تعریف نشده‌است.)

توان‌های منفی یک

توان‌های منفیِ یک بیشتر در دنباله‌های تناوبی کاربرد دارد.

اگر نمای عددِ منفیِ یک، فرد باشد، حاصل آن برابر خودش است: ${(-1)}^{2n+1}=-1$

اگر نمای عددِ منفیِ یک، زوج باشد، حاصل آن برابر یک است: 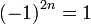${(-1)}^{2n}=1$

توان‌های اعداد حقیقی مثبت

به توان رساندن عددی حقیقی مثبت به توان یک عدد غیرصحیح را می‌توان به چند صورت به دست آورد:

عددی کسری تعریف کنیم و ریشه nام را به دست بیاوریم. این روشی است که در مدرسه‌ها از آن استفاده می‌کنند.
لگاریتم طبیعی تعریف کنیم و سطح زیر نمودار 1/x را به دست بیاوریم.

توان‌های کسری

از بالا به پائین: x^1/8, x^1/4, x^1/2, x¹, x², x⁴, x⁸.

در یک توان، با معکوس کردن نما ریشه آن بدست می‌آید. اگر $\ a$ عدد حقیقی مثبت و n عددی صحیح مثبتی باشد، داریم:

$\ x^n = a$

و ریشه nام $a$ نامیده می‌شود:

$x=a^{\frac{1}{n}}$

برای مثال: 8^1/3 = 2. حالا می‌توانیم توان 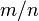$m/n$ را به صورت زیر تعریف کنیم:

$a^{\frac{m}{n}} = \left(a^{\frac{1}{n}}\right)^m$

hadi جمعه 13 دی 1392 ساعت 18:58

0 نظر

مثلث خیام-پاسکال

به آرایش مثلث‌شکل ضرایب بسط دوجمله‌ای، مثلث خیام، مثلت پاسکال، مثلث تارتالیا و مثلث خیام-پاسکال گویند.مثلث خیام را در برخی منابع به ندرت «مثلث خیام-پاسکال-نیوتن» نیز می‌گویند. این مثلث در زبان‌های گوناگون نام‌های دیگری نیز دارد در زبان انگلیسی «مثلث پاسکال»، ایتالیایی «مثلث تارتالیا» و در زبان چینی «مثلث یانگ هویی» نام گرفته‌است. در آثار متون سانسکریت پینگالا ریاضی‌دان هندی نشانه‌هایی از استفاده از این بسط دیده می‌شود. در همان دوران عمر خیام ریاضی‌دان ایرانی ادعای کشف روشی جبری برای به دست آوردن ضرایب بسط دوجمله‌ای می‌کند. کتاب «مشکلات الحساب»، کتابی که اثبات‌های این ادعا در آن آمده هنوز کشف نشده ولی در آثار طوسی تأثیر گرفته از او ضرایب را تا توان ۱۲ می‌توان دید بعد از او در قرن ۱۲ میلادی در آثار یانگ هویی ریاضی‌دان چینی، شکل مثلث به چشم می‌خورد. در قرن ۱۶ میلادی ریاضی‌دان ایتالیایی تارتالیا هم از خود این مثلث را به جا گذاشته و پس از یک قرن پاسکال ریاضی‌دان فرانسوی هم دوره با نیوتون روی این بسط و مثلث حسابی آن کار کرد.

hadi جمعه 15 آذر 1392 ساعت 13:21

0 نظر

ریاضیات برای دانش آموزان تیز هوش

ریاضیات برای دانش آموزان تیز هوش

درباره من

نظرسنجی

تقویم

ضرب چندجمله ای ها